Que représente cette gravure ? Un jeune homme regarde une estampe dans une galerie d'art. Mais on se rend compte, en tournant dans le sens inverse des aiguilles d'une montre, que la galerie fait partie de l'estampe observée. Le paysage devient de plus en plus large (effet de zoom arrière), jusqu'à représenter un port. En d'autres termes, le jeune homme observe un tableau dans lequel il se trouve lui-même. Les mathématiciens ont dit qu'ESCHER avait représenté là des surfaces de Riemann. N'allons pas plus loin !

La question qui se pose est la suivante: Pourquoi ne peut-on continuer à tourner? En effet, on tombe alors dans ce cercle non dessiné. Pourquoi Escher n'a-t-il pas terminé son dessin? Il y a deux catégories de réponses:

Ceux qui, comme Douglas Hofstadter, aujourd'hui professeur de sciences cognitives à l'université du Michigan (États-Unis) et auteur de l'ouvrage "Gödel, Escher et Bach, les brins d'une guirlande éternelle", pense que: "Si cette tache paraît être un défaut, le défaut est peut-être en fait dans nos attentes, car Escher n 'aurait pas pu finir cette partie du tableau sans violer les règles selon lesquelles il le dessinait". Et il conclut: "le centre de la spirale est, et doit être incomplet". "Cette idée me perturbait comme si on opposait une limite à l'esprit." (Texte cité par Azar Khalatbari dans son article nommé ci-dessous)

Ceux qui affirment qu'il y a une logique de continuité du dessin et qui ont cherché une solution. C'est cette démarche que Azar Khalatbari, une journaliste du magazine Science et Vie, relate dans son passionnant article du N° 732 de février 2008.


Ainsi, selon Sciences et Avenir :
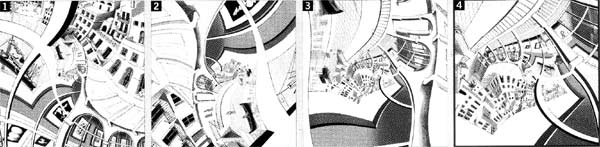
"Comment parvenir à combler le vide laissé au centre d'Exposition d'estampes? L'équipe de Hendrik Lenstra, de l'université de Leyde, a d'abord retrouvé la grille de torsion (à gauche) utilisée par l'artiste Maurits Cornelis Escher. Puis les chercheurs ont tenté de comprendre la structure mathématique qui se cachait dans ces tracés tortueux. Ils ont compris qu'il s'agissait d'une combinaison de plusieurs fonctions: dilatation, torsion, projection conforme - une opération qui conserve les angles de la grille. En utilisant ces règles mathématiques, ils ont calculé les différentes étapes de la reconstitution .... (1, 2, 3 et 4) qui ira se placer au centre d'Exposition d'estampes. Le dessin final (5), difficile à réaliser, est l'œuvre de l'artiste néerlandaise Jacqueline Hofstra."
Visiter aussi le site de l'université de Leyde (Pays-Bas)

ACHEVER L'INACHEVABLE

Voici la bande annonce du film de Jean Bergeron:

Pourquoi Escher n'a-t-il pas terminé le centre de son dessin lui-même? Voici ce que pense Jean Bergeron sur ce sujet:

"En ce qui concerne la capacité de Escher de terminer le dessin lui-même, il y a controverse et les moyens techniques de son époque ne l'aurait pas vraiment permis à sa satisfaction.

J'ai interviewé un de ses fils (George, celui qui a fait la paix avec son père) et le sujet est abordé. Voir dans les extras sur le DVD.
Détail intéressant, à la fin de sa période de pavages périodiques, il avait développé une aversion pour les personnages "à l'envers" comme les lutins - si bien qu'il s'est mis à ne dessiner que des pavages respectant la gravité. Je me suis demandé si la raison pour laquelle il n'avait pas terminé le dessin (outre la finesse extrême du trait) était que le personnage se serait trouvé la tête en bas. Possible, selon George, mais peu probable. Son souci premier était l'autoréférence.

Pour ce qui est de la solution, les mathématiques ont la qualité de ne pas avoir besoin de consensus. Ou bien c'est exact ou bien ça ne l'est pas. Et Lenstra a été à même de démontrer que sa solution est unique et exacte - les seules variantes sont les degrés de torsion et les "clics" de rencontre entre les lignes. Le côté le plus fascinant de tous est que ladite solution passe par un pavage périodique eschérien sur un plan imaginaire.
Je l'évoque dans le film, mais il aurait fallu un bon dix minutes pour expliquer en détail cet aspect des plus extraordinaires et tout à fait inattendu - d'où la magie de l'intuition humaine, thème sous-jacent du film."